統計の勉強-共分散

統計の問題集をちまちま解いているのですが共分散の所でちょっと詰まった。

問題としては独立な二つの正規分布(norm1, norm2)があり、それらの分散は何れも１。

このとき、norm1と(norm1+norm2)/√2の共分散を求めよ、という感じ。

回答みても直感的に理解できなかったのでrで書いてみる。

#norm1 <- rnorm(10000, mean = 100, sd = 1)　
#norm2 <- rnorm(10000, mean = 1000, sd = 1)

#散布図を作成し平均を描画
plot(norm1,norm2)
abline(h = mean(norm2),v = mean(norm1),col = "red")

まず分散1で適当な正規分布を2つ作成。

 散布図はこうなる。赤線はそれぞれの平均。

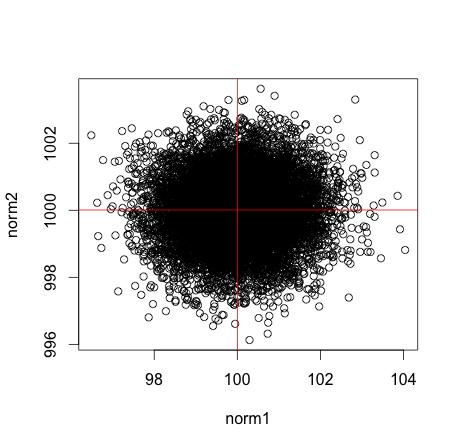
ここで相関係数は

"散布図に平均点で縦横に軸を描き込んで、プロットされている各人の点からそれぞれの軸に下ろした垂線と軸とで囲まれた長方形の（正負つきの）面積の平均"

相関係数のわかりやすい解釈（続き） - たけみたの脱社会学日記

なので適当に外れ値選んで長方形を書く。

# 外れ値において長方形作成
polygon( c(norm1[which.max(norm1)],mean(norm1),mean(norm1),norm1[which.max(norm1)]) ,c(mean(norm2),mean(norm2),norm2[which.max(norm1)],norm2[which.max(norm1)]), col="gray")

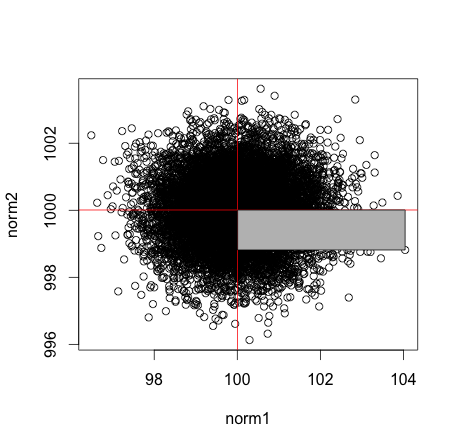
これらの分布に相関はないので共分散は0.

次にnorm2を(norm1+norm2)に変更し同様の解析。

# norm1,norm2+norm1で同様の処理
plot(norm1,(norm2+norm1))
abline(h = mean(norm2+norm1),v = mean(norm1),col="red")
polygon( c(norm1[which.max(norm1)],mean(norm1),mean(norm1),norm1[which.max(norm1)]) ,c(mean(norm2+norm1),mean(norm2+norm1),norm2[which.max(norm1)]+norm1[which.max(norm1)],norm2[which.max(norm1)]+norm1[which.max(norm1)]), col="gray")

norm1が足された分、すべての点はY軸方向正の方向へ移動し、相関が出てくる。

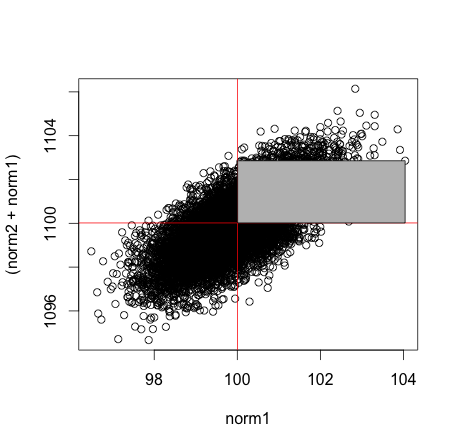
ここで今回の図と最初の図の長方形の面積の差を考える。

最初の図の長方形は

(norm1-norm1の平均)*(norm2-norm2の平均)

二番目の図の長方形は

(norm1-norm1の平均)*{(norm1+norm2)-(norm1の平均+norm2の平均)}

この差分を取るとnorm1^2-norm1の平均^2(=norm1の分散)となる。

よって今回の共分散はnorm1の分散と等しく1。

ここまではOK。次はnorm1と(norm1+norm2)/√2でやってみる

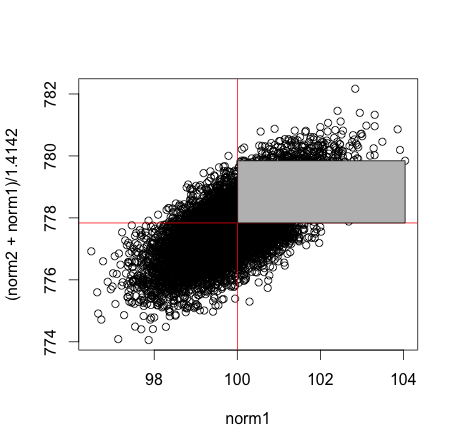
おっとそうか図が変わらないのか。元々norm1とnorm2に相関無いから共分散に影響を与えるのはこの場合もnorm1の分散で、面積としてはy軸が1/√2になってるので今回の分散はnorm1の分散/√2 = 1/√2。

なんかグラフィカルに理解しないと頭に入ってこない。

確率変数の計算得意になりたい。

#適当な正規分布作成
norm1 <- rnorm(10000, mean = 100, sd = 1)　
norm2 <- rnorm(10000, mean = 1000, sd = 1)


#散布図を作成し平均を描画
plot(norm1,norm2)
abline(h = mean(norm2),v = mean(norm1),col = "red")
which.max(norm1)

# 外れ値において長方形作成
polygon( c(norm1[which.max(norm1)],mean(norm1),mean(norm1),norm1[which.max(norm1)]) ,c(mean(norm2),mean(norm2),norm2[which.max(norm1)],norm2[which.max(norm1)]), col="gray")


var(norm1,norm2)

# norm1,norm2+norm1で同様の処理
plot(norm1,(norm2+norm1))
abline(h = mean(norm2+norm1),v = mean(norm1),col="red")
polygon( c(norm1[which.max(norm1)],mean(norm1),mean(norm1),norm1[which.max(norm1)]) ,c(mean(norm2+norm1),mean(norm2+norm1),norm2[which.max(norm1)]+norm1[which.max(norm1)],norm2[which.max(norm1)]+norm1[which.max(norm1)]), col="gray")



#norm1が足された分、すべての点はY軸方向正の方向へ移動し、相関が出てくる

var(norm1,(norm1+norm2))
sum((norm1-mean(norm1))*( (norm1+norm2)-mean( (norm1+norm2))))/10000



plot(norm1,(norm2+norm1)/1.4142)
abline(h = mean(norm2+norm1)/1.4142,v = mean(norm1),col = "red")
sum((norm1-mean(norm1))*( (norm1+norm2)/1.4142 -mean( (norm1+norm2)/1.4142)))/10000
polygon( c(norm1[which.max(norm1)],mean(norm1),mean(norm1),norm1[which.max(norm1)]) ,c(mean((norm1+norm2)/1.4142),mean(norm1+norm2)/1.4142,(norm2[which.max(norm1)]+norm1[which.max(norm1)])/1.4142,(norm2[which.max(norm1)]+norm1[which.max(norm1)])/1.4142), col="gray")