MacにBiopythonをインストール(python3)
jupyter notebookが最高なのでpythonを3系統に移行しています。
python3でのBiopythonのインストールをしたのでメモ。
何パターンか試しましたが、結果としてpip3使うのが一番楽でした
curl -O http://python-distribute.org/distribute_setup.py sudo python3 distribute_setup.py curl -O https://raw.github.com/pypa/pip/master/contrib/get-pip.py sudo python3 get-pip.py pip install biopython
2016年総括
年の瀬に今年一年を振り返っておこう。
・趣味
とにかくポケモンにハマった一年だった。完全にポケモンGOの影響。
ポケモンスタンプラリーも行ったしサンムーンも買ったしポケモンカードも嗜んだ。
生まれて初めてミュウツーの逆襲を見て、引くくらい泣いた。
ボードゲームがあまりやれない年だった。研究室絡みで数回やれたのはよかったけど。
なぜボードゲームをやらなくなったかというと仲間内で1年半ぶりぐらいにMTGが再燃したということがあり、
ボードゲーム仲間の多くがMTG(マジックザギャザリング)に流れたというのがある(僕含む)。
映画をあまり見ない年だった。アマゾンプライムやHuluやNetflixは入れ替わり契約していたのだが、
僕としては珍しくアニメを見ることが多かった。魔法陣グルグルはNetflixの無料期間二週間で2シリーズ全話見た(50話くらい?)。
当然ポケモンも見た。
・健康
割と筋トレを真面目に始めた。
プッシュアップバーの導入と、プロティンでカロリーコントロールすることを始めたのが大きい。
有酸素運動も、1時間ぐらいならさほど無理せず走れるようになった。
健康的な生活を送れば意識せずとも煙草の量が減ることを発見した。正のフィードバックループ。
・研究
今年はそれなりに実りあった気がする。
今年の5月ぐらいまでは結果が出るか出ないかわからないような実験をずっとやっていたのだけれど、
6月ぐらいにこれじゃアカン卒業できないと思い今あるデータからストーリーを組み立てようと思い直す。
今はそれから半年ぐらいかかってほぼ論文書きあがった段階だけど、思っていたよりいいものが書けていると思う。
来年頭には投稿できるといいのだが。
・人間関係
今年何より衝撃だったのが友人Nがタイ人と結婚したことだ。
N君は昔一緒にバンドやってた仲間で、大学中退して就職してタイで働いていた。
そこで今の奥さんと出会ったらしいのだが、この話には面白いポイントが3点ある。
①その奥さんがタイの田舎の方の酪農家の娘で、N君は現在タイの田舎に土地と痩せた牛を3頭持っていること。
②その村に伝わる結婚の儀式で、夫婦そろって土に埋められている周りを村人が踊っていたこと。
③友人Nがタイ語も英語も大して話せないこと。
③に関しては不可解のようにも聞こえるが、友人Nは底知れずアホな代わりに「現在の状況をどこまでも受け入れる」という類稀なる能力を持っていることから説明がつく。
思うに、彼は名作映画「イエスマン」でジムキャリー演じる主人公カークのように、タイ語や英語で来たよくわからない質問に全て「yes」と答えていたのだろう。“YES”は人生のパスワードである。何か行動を起こす前にどうしても下らない損得勘定を挟んでしまう自分を恥じ、初めて彼に尊敬の念を抱くようになった。
来年の新年会でN夫婦と初めて会えることになったので、彼らに心からの祝福の念を伝えたい。
もっとあった気もするけど思い出せないのでこんなもんです。
過去を振り返る作業は基本的に苦手です。
今年読んだ一番好きな論文2016
多くの人々はじめまして。@Yohei__Kです。駄ブログへようこそ。
現在博士後期課程で海洋微生物の研究をしつつ、生命情報若手の会のスタッフをやったり、ポケモン(サン)をやったり、ポケモン(GO)をやったりしています。MTGとボードゲームと音楽関係は最近全然やれてなくて悲しいので適当に誘ってください。よしなに。
今年読んだ一番好きな論文2016、たのしそうだったのでエントリーしてみましたが、どんな分野の人が見てるのかよくわからないのでとりあえず分野の紹介的なところからざっくりと始めようかと思います。微生物系の人すくなそうだし・・・
まず、僕の思う環境微生物研究の醍醐味として、「見えない世界をどう想像できるか?」というものがあります。
例えば、有名な研究として、海の微生物には大きく「自由生活性(水中を漂う)」と「付着生活性(マリンスノーとかにくっつく)」の二つの生き方があり、細菌群によって好みが違う、という論文があります(Delong et al. 1993)。
Delong先生は異なるサイズのフィルターでろ過することで、海水を自由生活性の細菌が含まれる画分と付着生活性の細菌が含まれる画分に分け、それぞれの画分の細菌群衆が大きく異なるということからこの仮説を提唱しました。
この研究によって、これまで漫然と一様な環境のように考えられてきた海洋表層の水塊にも微小な環境が存在し、細菌はそれぞれ微小なニッチに適応して棲み分けているということがわかりました。
この研究のように、「見えないぐらい小さい生き物の視点から見ると、海という環境はどんな環境なのか?」というのを想像し、適切な手法によってそれが正しいことをNatureに問うような研究はカッコイイ研究だと思います。
また、僕はどちらかというと環境よりも生物の側に興味があるので、提示された「微生物にとっての海という環境」に関する新しい見方が、生物の進化や生理生態を理解する上で重要であればよりクールだと感じます。
そんな視点から、今年読んだ一番面白い論文を選びました。
論文は以下です。ReviewですけどOriginal paperじゃないとダメって書いてなかったので多分大丈夫なのでしょう。
小学校の読書感想文にドラクエの攻略本を選んでも大丈夫だったので、きっと今回も許される。
Lightning-triggered electroporation and electrofusion as possible contributors to natural horizontal gene transfer
「雷により生じる電気穿孔と電気融合は遺伝子水平伝播の要因になるかもしれない」
Tadej Kotnik
前これについて呟いたのでTwitterで僕をフォローしてる人は覚えがあるかもしれない。
雷により自然発生するエレクトロポレーションが細菌の水平伝播を引き起こす可能性に関する論文。スゲェこと考える人がいるなぁ https://t.co/yvdeFSQk4n
— くまがい (@Yohei__K) 2016年9月12日
ある程度専門近い人はもうこのタイトルだけで全てなので僕が何か言うこともない気がします。
なるべくこの興奮を分野外の人に伝えるべくこの駄ブログの駄エントリを書いています。
電気穿孔法(エレクトロポレーション)っていうのは遺伝子操作やる人にとってはおなじみの手法で、「細胞懸濁液に電気パルスをかけることで細胞膜に微小な穴を空け、DNAを細胞内部に送り込むことで、形質転換する」 電気穿孔法 - Wikipediaというかなり古典的な技術です。
このレビューでは電気穿孔が雷において自然界でも生じていて(Lightning-triggered electroporation)、それが細菌の遺伝子水平伝播の駆動要因のひとつである可能性、また生命進化の初期段階においてLightning-triggered electroporationは特に重要だった可能性を論じています。
著者のTadej Kotnik(google scholarリンク)さんは膜電位の専門家のようで、この仮説に関する論文を既にたくさん出しています。なので、その分野の第一人者が自身の研究を振り返るような感じでしょうか。
レビューの最初の項目からしてかっこいいのでその冒頭を訳します。
はじめに:生物の分類の起源から系統樹へ
彼らの生活環境の中にある「生物」と「非生物」に名前をつける作業は、人類の文明の始まりと密接に関係しています。
7万7千年以上前に遡る抽象的思考の発達によって、漁師たちは自分たちの取っているものが単なる「魚」ではなく、そこに存在するいろいろなタイプを区別するようになりました。また、「様々な種類の生物の中にはさらに様々な種類の肉が存在している」といった、入れ子構造を持った生物の捉え方をするようになりました。
まぁ博物学や生物学の歴史というような文脈では良く聞くような話です。
僕はひねくれているので進化の人にこういう文章書かれると「ケッ、なんかいけすかねぇ野郎だなぁ」と思ってしまいがちなのですが、
膜電位の生物物理の人がこういう文章書いてるのはキュンときます。
「分子進化のヤツらだけに進化は語らせない。生命の本質は膜構造だ!膜の専門家である俺から進化を語らせてもらう!」という矜持を勝手に感じてますが、雑誌が「Physics of Life Reviews」という生物物理系のレビュー誌なので「生物物理業界において進化を語る変わり者」くらいの感じかもしれません。それもカッコいいな。
ここからアリストテレス、コンラート・ゲスナー、リンネと分類の歴史がなかなか力強い筆致で語られていきます。
楽しんで書いてるのがひしひしと伝わってきてなかなか味わい深いのですが、(たいした話じゃないし)キリがないのでその辺はバッサリ割愛します。
その流れで、進化の話になります。
系統樹のような構造だけでなく、細胞内共生のような系統樹の異なる枝のリンクが重要であること、またそのようなリンクとして重要な要素に遺伝子水平伝播があることを説明します。
彼曰く、遺伝子水平伝播の要因を大別すると以下の三つになるそうです。
「細菌の接合伝達」「ウイルスの感染」「天然の外来DNA取り込み能力」
さらにざっくりと言えば「細菌-細菌」、「ウイルス-細菌」、「環境中のDNA-細菌」の三つってことでしょうね。
Gene Transfer Agentとか微妙なやつをどっかに入れ込めばまぁ間違ってはないかなという感じです。
で、ここに彼は4つめの要因として、
「雷」
を提案したいと。毛色が違う!(カッコいい!)
このアイディアは新しいものではなくて、1990年の異種細菌間の電気穿孔によるDNA伝達の論文のディスカッションでは「We speculate...」に続けて、1995年の細菌の進化に関するレビューでは「... is an interesting concept.」の形で、
「もしかしたら雷みたいな要因で自然界でこういうことが起こってて遺伝子水平伝播の要因になっててもおかしくないよねアハハハハ」
みたいなことが書いてあるようです。
よくある、「面白いけど証明の仕方がよくわからない仮説で、飲み会とかではちょいちょい話されるネタ」って感じでしょうか。
10年以上長らく誰もまともに取り合わず検証もされなかった仮説ですが、2001年にこの仮説を実験的に示そうという(酔狂な)グループが現れます。彼らは土壌由来の微生物群衆と薬剤耐性菌を混ぜて電圧をかけると、新規に薬剤耐性を獲得する株が増加することを報告しています。
しかし、著者曰く「彼らの研究はどれもあまりコミュニティの興味を引かず、この研究分野が確立されるまでには至らなかった」とのことです。2001年の論文は一応50回以上引用されてるしそれなりかなと思ったんですが、「この分野を作ったのは俺だ!」ってことでしょうか。
ここから電気穿孔の理論的な部分に突入します。「どれぐらいの電圧がかかると細胞がどうなるか」の概略図が印象的でグッときます。
ざっくり説明すると以下のような感じです。
10^3 > 電圧E(V/cm)
普通の細胞状態
10^4 > 電圧E(V/cm) > 10^3
プラスミドやタンパクなどの低分子が出入りできる、小さい穴が細胞膜に生じる
10^5 > 電圧E(V/cm) > 10^4
穴がでかくなって染色体とかリボソームとかも出て行くようになる
電圧E(V/cm) > 10^5
DNA、タンパク、リボソームなどが軒並みぶっ壊れる
なるほどわかりやすい!(見れる人は元論文見て!)
この図を見るだけで、「DNAが通るのに充分なサイズの穴が開く」かつ「受け取り手の細胞が死なない」という、エレクトロポレーションに必要な条件がギリギリのところで決まってることがイメージできます。
(生物種によってめちゃくちゃ細かく電圧の条件が決まっていることは、エレポ経験者の方はご存知かと思います)
で、次に来るのが「Cell electrofusion (細胞電気融合)」の話です。
僕は知らない現象でしたが、電気穿孔と原理としては似通っています。
細胞膜同士が触れ合っている時に電気穿孔が開くと、触れ合った膜同士が融合するそうです(これもわかりやすい図がある)。
細胞融合の研究では一般的な手法とのこと。知らなかった。
細胞電気融合に関しても電気穿孔と同様にどれぐらいの電圧がちょうどいいのか、実験的にも理論的にも研究が進んでいるようです。
そして肝心の雷ですが、雷が落ちた時に、どれぐらいの範囲にどれぐらいの電圧がかかるかを計算します。
これに関しては雷自体の性質(電流の強さや時間など)を固定してしまえば電気伝導度σから求めることができます。
これを計算すると、淡水の電気伝導度(σ < 1 )程度ではだいたい雷の落ちた場所から数センチ~10数センチ離れたところに電気穿孔・電気融合が生じるのにちょうどいい層ができるようです。層の厚みは数10センチ~数メートル程度のようなので、細菌の密度によってはこの中で水平伝播が生じてもおかしくはない気がします。特に論文中では議論されてないですが、細菌は水圏では一様分布するわけではなく、ダマになっていて局所的に高密度に分布していたりするので、そういう場所ではより起こりやすくなったりしそうですね。
ちなみに海水では電気伝導度の範囲が20 < σ < 60とグッと上がるため、電気穿孔・電気融合が生じる層の厚みは数10ミリ~数センチ程度とだいぶ下がります。これだとさすがにそうそう起きないかなぁ。
これらのことから著者は「下水みたいな、淡水かつ菌体密度が高い環境が一番雷による水平伝播が起きやすいんじゃないか」と言っています。
下水道に雷が落ちて遺伝子の水平伝播が起きている絵はディストピアSFのオープニングのような情緒があってアツいですね。
なかなか恐ろしいミュータントが生まれそうです。
また、彼はMulkidjanian et al. 2012の「生命は陸水で生まれた説」を引用し、「もしそうなら初期生命においては雷による遺伝子水平伝播がめちゃくちゃ起きてたかもね!」と言ってます。ここまでくると仮定に仮定が重なりすぎてどうリアクション取ったらいいか分からなくなってきますが、夢はあるので無粋なコメントは避けます。
感想です。
・雷の駆動するエレクトロポレーションは起こっててもおかしくない
・しかし他のメカニズムに比べたらだいぶレアな現象だろう
・物理的なプロセスなので、生物学的には無理のあるような種間における遺伝子水平伝播とかを考えると重要かもしれない
・何かしら配列ベースの進化の話と繋がれば激アツなんだけど難しいだろう
・細菌の目線から「雷」という自然現象を捉え直したのはカッコよさある
・こういう飲み会レベルのアイディアをまじめに考えてカッコよく語れる大人になりたい
以上!
iTolの使い方
最近やたら論文にかっちょいい系統樹載ってるなぁと思うと大体iTolで書かれてることが多いと思うのですが、あんまりわかりやすい解説がないので試行錯誤の内容をメモっていく。
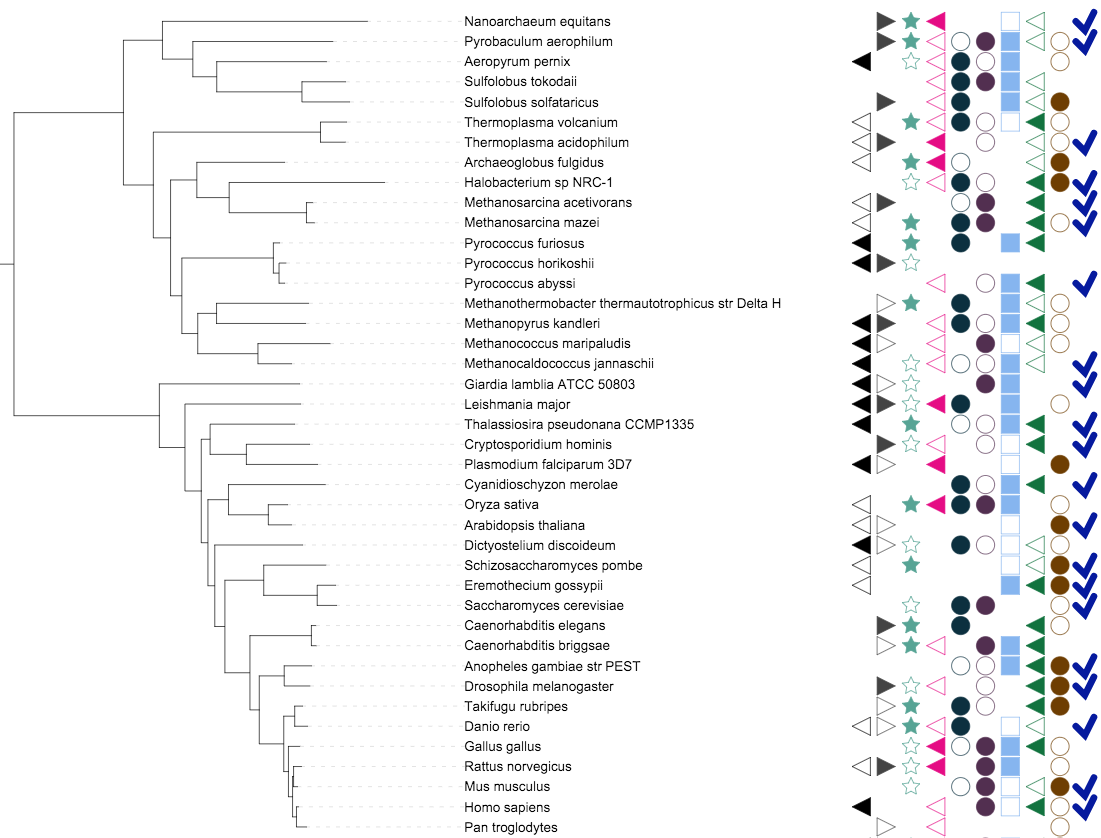
目標はこんなやつ書くこと
・登録が必要
・挙動はブラウザに依存するっぽい(僕の環境ではSafariだといけてFirefoxはダメだった)
・データセットファイルのテンプレートはhelpページからダウンロードできる
・データセットの追加には+ボタンをクリック
・データセットのテンプレートの意味を理解するのがめんどい
・phylotoastにiTolのデータセットを作るスクリプトがある(iTol.py)
Welcome to PhyloToAST documentation! — PhyloToAST 1.3.0 documentation
-しかしインストールがむずい
-phylotoastを使うにはbiom-formatが必要
・biom-formatのインストールでも若干詰まる
これだとエラーが出る
pip install biom-format
これだとなぜかいけた
pip install https://pypi.python.org/packages/source/b/biom-format/biom-format-1.3.1.tar.gz
・しかしiTol.pyの入力ファイルの形式(biom-format)の理解がやたら面倒そうなことにここで気づく
・スクリプト使わず自分でテンプレートを書き直した方が早い
以下Binaryのテンプレートに自分なりのコメントを残しておく
#おまじない DATASET_BINARY #区切り文字。好み SEPARATOR TAB #legendの設定 どうせあとでイラレで付けるから適当 DATASET_LABEL label1 COLOR #ff0000 #それぞれのカラムをどんな記号にするか #1: rectangle #2: circle #3: star #4: right pointing triangle #5: left pointing triangle #6: check mark FIELD_SHAPES 1 2 3 4 #カラムの名前の設定 FIELD_LABELS f1 f2 f3 f4 #カラムの色の設定 FIELD_COLORS #ff0000 #00ff00 #ffff00 #0000ff #これ以外の設定はwebのインターフェイス上で変えられるらしいからとりあえずはいいや #それぞれのカラムについて、0:open symbol 1:closed symbol -1: nothing DATA 01 1 0 -1 0 02 1 0 -1 0 03 1 0 -1 0 04 1 0 -1 0 05 1 0 -1 0 06 1 0 -1 0 07 1 0 -1 0
Rでサンプル数の違う二群を一つのファイルとして無理矢理読み込む
setwd ("hogehoge") #入力は以下のような感じ #A+ 0.2 0.5 0.2 0.7 0.9 #A- 0.5 0.6 0.1 0.5 0.6 1.2 3.0 0.8 #B+ 0.2 0.5 0.2 0.7 0.9 #B- 0.5 0.6 0.1 0.5 0.6 1.2 3.0 0.8 dat1<-read.delim("hugahuga.tsv", sep="\t", stringsAsFactors=FALSE, header=FALSE, na.strings="",row.names = 1) #箱ヒゲ書いてみる dat1 <- t(dat1) boxplot(dat1)
BioPythonで系統樹を書いてNewick出力
タイトルの通り。
MegaよりもSeaViewよりも軽いし落ちない。
#!/usr/bin/env python #coding: UTF-8 #よく使うモジュールは何も考えずに書く import sys import re import os import glob import copy import commands from bisect import bisect from Bio import SeqIO import urllib2 import datetime import matplotlib from Bio import Phylo from Bio.Phylo import NewickIO from Bio import Entrez argvs = sys.argv # コマンドライン引数を格納したリストの取得 argc = len(argvs) # 引数の個数 #name = argvs[1] from Bio.Phylo.TreeConstruction import DistanceCalculator from Bio import AlignIO aln = AlignIO.read('hogehoge.fasta', 'fasta') #print aln #SingleLetterAlphabet() alignment with 5 rows and 13 columns calculator = DistanceCalculator('identity') dm = calculator.get_distance(aln) from Bio.Phylo.TreeConstruction import DistanceCalculator, DistanceTreeConstructor constructor = DistanceTreeConstructor(calculator, 'nj') tree = constructor.build_tree(aln) print tree Phylo.write(tree, 'hugahuga.tre', 'newick')
nt、env_ntデータベースから相同性ベースで配列を取り出す
ある遺伝子ホモログについて、代表配列20個程度がある状態がスタート。
この配列をnt、env_ntデータベースに投げてヒットした領域をmulti fastaとして取り出したい。そんなのしょっちゅうやってるよと思ったが意外とめんどくさかった。
なんでかというとファイルのデカさ。ntより小さめのenv_nt でさえ100GB以上ある。このサイズだと大好きなSeqIO.parseで処理できない。どうしよう。分割して保存したらサーバー上の僕の領域が確実にパンクする。
アプローチを変えてみる。遺伝研スパコンの力でblastはいけたので、ヒットした配列のGenBank IDを取得。http://www.ncbi.nlm.nih.gov/nuccore/**のアドレスからソースを取得し無理矢理配列をゲットしようと思ったがあまり美しくないなと思い直し、biopythonでできないかしらと調べるとコードまで出てきてハッピー。
Fetching Genbank Entries For List Of Accession Numbers.
リンク先のコードのrettype="gb"をrettype="fasta"にすれば万事解決。